|
HOME
FACULTY
STUDENTS
RESEARCH
PUBLICATIONS
COURSES
|
RESEARCH > Quasi-normal modes
>
Black holes in asymptotically flat space
The study of quasi-normal modes in asymptotically flat space-times has attracted
a lot of attention recently [15,16,17,18,19] because the asymptotic form of quasi-normal
frequencies was shown to be related to the Barbero-Immirzi parameter [20] of Loop Quantum Gravity (see [21] and references therein).
The asymptotic form of high overtones is
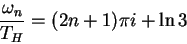 |
(3) |
This has been derived numerically [22,23]
and subsequently confirmed analytically [15].
The imaginary part is large making the numerical analysis cumbersome, but
is easy to understand by noting that the spacing of the frequencies 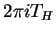 coincides with the spacing of the poles of a thermal Green function on the
Schwarzschild black hole background.
The analytical value of the real part was first conjectured by Hod [24]
based on the general form of the area spectrum of black holes
proposed by Mukhanov and Bekenstein [25] (
coincides with the spacing of the poles of a thermal Green function on the
Schwarzschild black hole background.
The analytical value of the real part was first conjectured by Hod [24]
based on the general form of the area spectrum of black holes
proposed by Mukhanov and Bekenstein [25] (
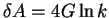 , ,
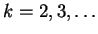 , where , where 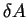 is the spacing of eigenvalues and is the spacing of eigenvalues and
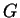 is Newton's constant in units such that is Newton's constant in units such that 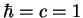 )
which is related to the number of microstates of the black hole through
the entropy-area relation )
which is related to the number of microstates of the black hole through
the entropy-area relation
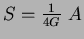 [26]. It has an intriguing value
from the loop quantum gravity point of view suggesting that the gauge group
should be
SO(3) rather than
SU(2) (since we have
k = 3 instead of
k = 2). Thus the study of quasi-normal modes
may lead to a deeper understanding of black holes and quantum gravity. [26]. It has an intriguing value
from the loop quantum gravity point of view suggesting that the gauge group
should be
SO(3) rather than
SU(2) (since we have
k = 3 instead of
k = 2). Thus the study of quasi-normal modes
may lead to a deeper understanding of black holes and quantum gravity.
Motl and Neitzke [15] showed that (3) may be extended to
arbitrary spin
j and analytically derived the generalized expression
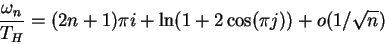 |
(4) |
Their derivation
offered a new surprise as it heavily
relied on the black hole singularity. It is intriguing that the ``unphysical''
region beyond the horizon influences the behavior of physical quantities.
Dr. Siopsis and Dr. Musiri extended the result of ref. [15] by calculating the first-order
correction to the asymptotic formula (4). They solved the wave equation
perturbatively for arbitrary spin of the wave and obtained an explicit
expression for the quasi-normal frequencies [27],
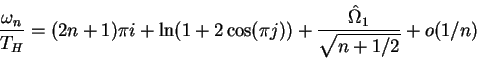 |
(5) |
where
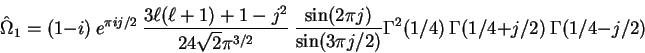 |
(6) |
which includes the 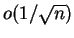 correction to the correction to the 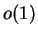 asymptotic formula (4).
This result is in agreement with
numerical results [23,18] in the case of gravitational and scalar
waves as well as results
from a WKB analysis [19] in the case of gravitational waves. asymptotic formula (4).
This result is in agreement with
numerical results [23,18] in the case of gravitational and scalar
waves as well as results
from a WKB analysis [19] in the case of gravitational waves.
Extending the above calculation to rotating (Kerr) black holes appears to be far from straightforward. One needs to solve a set of coupled differential
equations, because the angular and radial equations do not neatly separate as
in the Schwarzschild case [28].
Based on Bohr's correspondence principle, Hod has argued [29] that
the real part of the quasi-normal frequencies of gravitational waves
ought to be given by the asymptotic expression (cf. eq. (3))
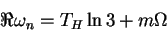 |
(7) |
where 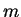 is the azimuthal eigenvalue of the wave and is the azimuthal eigenvalue of the wave and 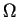 is the
angular velocity of the horizon.
On the other hand, numerical results have been obtained [17] which
appear to contradict the above assertion, suggesting instead an asymptotic
expression independent of the temperature, is the
angular velocity of the horizon.
On the other hand, numerical results have been obtained [17] which
appear to contradict the above assertion, suggesting instead an asymptotic
expression independent of the temperature,
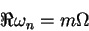 |
(8) |
To shed light on this issue, Dr. Siopsis and Dr. Musiri
obtained an expression for the asymptotic form of quasi-normal modes of
a Kerr black hole [30] by solving the Teukolsky wave equation [28] and applying a monodromy argument similar to the Schwarzschild case [15].
The equation reduced to Whittaker's equation and the final expression was in
agreement with Hod's formula (7). However, this result is only valid
for asymptotic values of 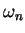 which are bounded from above by which are bounded from above by 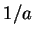 ,
where ,
where 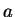 is the angular momentum per unit mass of the Kerr black hole.
Thus, its validity is limited to small values of the parameter is the angular momentum per unit mass of the Kerr black hole.
Thus, its validity is limited to small values of the parameter 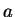 . This
includes the Schwarzschild limit in which the range of frequencies extends to
infinity. It appears that Bohr's correspondence principle is not applicable
to the true asymptotic regime . This
includes the Schwarzschild limit in which the range of frequencies extends to
infinity. It appears that Bohr's correspondence principle is not applicable
to the true asymptotic regime
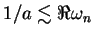 in general and the
numerical result (8) may well be valid. Understanding it analytically
is a challenge. in general and the
numerical result (8) may well be valid. Understanding it analytically
is a challenge.


|
![]()
![]()
 Department of Physics and Astronomy
Department of Physics and Astronomy![]()
![]()