Strings and Quantum Gravity

THEORETICAL HIGH ENERGY PHYSICS
Strings and Quantum Gravity

HOME
FACULTY
STUDENTS
RESEARCH
PUBLICATIONS
COURSES
RESEARCH > Quasi-normal modes > Black holes in AdS space
On account of the AdS/CFT correspondence, these quasi-normal modes are expected to correspond to perturbations of the dual CFT. The establishment of such a correspondence is hindered by the difficulties in solving the wave equation. In three dimensions, the wave equation is a hypergeometric equation and can therefore be solved [11]. In higher dimensions, the wave equation turns into a Heun equation which is unsolvable. Numerical results have been obtained in four, five and seven dimensions [12].
Dr. Siopsis and S. Musiri developed an analytic method of solving the wave equation, which is in general a Heun equation [13], in the case of a large black hole living in AdS space. The method is based on a perturbative expansion of the wave equation in the dimensionless parameter 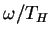$\omega / T_H$ , where 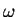$\omega$ is the frequency of the mode and 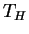is the (large) Hawking temperature of the black hole. 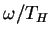Such an expansion is no trivial matter, for the dependence of the wavefunction on $\omega / T_H$ changes as one moves from the boundary of AdS space to the horizon. 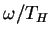The zeroth-order approximation was chosen to be an appropriate hypergeometric equation so that higher-order corrections were indeed of higher order in $\omega / T_H$ . In three dimensions, this hypergeometric equation is exact. In five dimensions, it was shown that the low-lying quasi-normal modes obtained from the zeroth-order approximation were in good agreement with numerical results [12]. The first-order correction was also calculated. The method in [13] may be applied to higher dimensions but the convergence of the perturbative expansion appears to be slower. It would be interesting to examine the implications of this perturbative approach for the AdS/CFT correspondence.
Dr. Siopsis and S. Musiri also investigated an approximation to the wave equation which was valid in the high frequency regime [14]. In five dimensions they showed that the Heun equation reduces to a Hypergeometric equation, as in the low frequency regime [13]. They obtained an analytical expression for the asymptotic form of quasi-normal frequencies in agreement with numerical results [12],

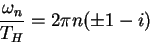$\begin{displaymath}\frac{\omega_n}{T_H} = 2\pi n(\pm 1-i) \end{displaymath}$ (2)

in five dimensions. These expressions in three and five dimensions may also be easily obtained by considering the monodromies around the singularities of the wave equation. These singularities lie in the unphysical region. In three dimensions, they are located at the horizon r = r_h, where r_h is the radius of the horizon, and at the black hole singularity, r = 0. In higher dimensions, it is necessary to analytically continue r into the complex plane. The singularities lie on the circle |r| = r_h. The situation is similar to the case of asymptotically flat space where an analytic continuation of r yielded the asymptotic form of quasi-normal frequencies [15]. It is curious that unphysical singularities determine the behavior of quasi-normal modes. Unfortunately, the wave equation possesses more than two singularities. Thus, a simple monodromy argument such as the one applied to three and five dimensions [14] does not appear to be applicable. Work in this direction is in progress.

___________________________________________________

Department of Physics and Astronomy e-mail: siopsis AT tennessee DOT edu

Voice: (865) 974-7859 Fax: (865) 974-7843

401 Nielsen Physics Bldg., The University of Tennessee, Knoxville, TN 37996-1200, U.S.A.