

g is a dimensionless coupling constant where
![]() (length2).
This series is valid for smalll g and breaks down when g is large, eg.
black holes or low energy case. Before considers strings at strong coupling let
look at a simple black hole, Schwarzschild black hole.
(length2).
This series is valid for smalll g and breaks down when g is large, eg.
black holes or low energy case. Before considers strings at strong coupling let
look at a simple black hole, Schwarzschild black hole.
Schwarzschild black hole
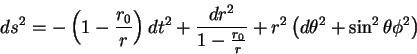 |
(1) |
| (2) |
| (3) |
| dU | = | TdS | (4) |
| = | 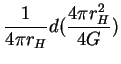 |
||
| = | 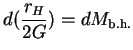 |
(5) |
| u | T4 | ||
| U | = |
| r0 | |||
| T | |||
| S | 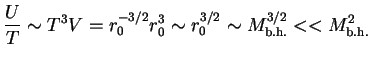 |
(6) |
| H | |||
| M2 | 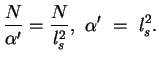 |
#1#2#3#4#5
@font#1#2pt
#3#4#5

Strings live in D dimensions, therefore there are D possible directions for strings to move to or
![]() , for n steps, Dn possiblities, ie.
, for n steps, Dn possiblities, ie.
| S | |||
| = |  |
||
| S | Mls | (7) |
![]() (i) If g small, then string perturbation thoery is still valid.
(i) If g small, then string perturbation thoery is still valid.
![]() (ii) If g large(ls small) or M
(ii) If g large(ls small) or M![]()
![]() increase, then ls
small enough ls
increase, then ls
small enough ls![]() r0 and
r0 and
![]()
![]()
![]()
![]()
![]() .
Then S
.
Then S
![]()
![]() and
and
| M2. | (8) |
Next let consider Kaluza-Klein black hole with the metric and following properties
| ds2 | = | 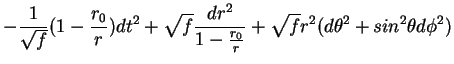 |
(9) |
| f(r) | = | 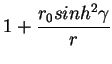 |
(10) |
| h(r) | = | 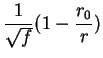 |
|
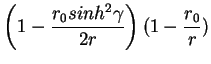 |
|||
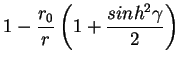 |
|||
| 2GM | = | 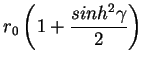 |
(11) |
| TH | = | 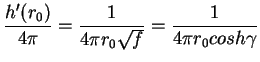 |
(12) |
| AH | = | (13) | |
| Q | = | 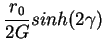 |
(14) |
| n | = | 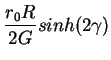 |
(15) |
| p | = | ||
| Q | = | 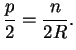 |
The 10 dimensional Kaluza-Klein metric, reduced to 4-D, and its properties are
| ds2 | = | 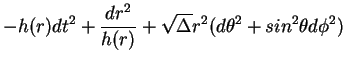 |
(16) |
| h(r) | = | 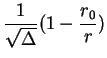 |
|
| = | f1 (r)f2 (r)f3 (r)f4 (r) | (17) | |
| Qi | = | 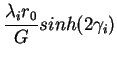 |
(18) |
| = | 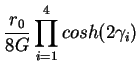 |
(19) | |
| S | = | 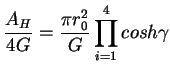 |
(20) |
| TH | = | 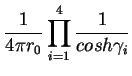 |
(21) |
| dU | = | 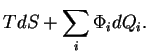 |
(22) |
If consider in an extremmal case, with fixed Qi, r0
![]() 0, then
0, then
![]()
![]()
![]() and
and
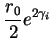 |
|||
| = |  |
||
| S | = | 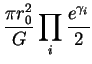 |
|
| = | 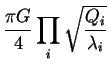 |
(23) | |
| M | 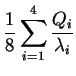 |
(24) | |
| TH | = | 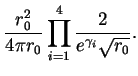 |
(25) |
From string theory, six dimensions are compactified. Let try to do different combinations of D-brane.
#1#2#3#4#5
@font#1#2pt
#3#4#5

Ri, i = 1,...,6, compactified dimension index. D6-brane is on
(x1 ,..,x6 ) with Q1,
D2-brane is on
(x1 ,x2 ) with Q2, and D5-brane is on
(x2 ,..,x6 ) with Q3, where pi = n/Ri.
And count the states on the branes. The entropy and
![]() will be
will be
| S | = | 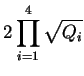 |
(26) |
| = | 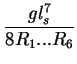 |
||
| = | 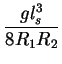 |
||
| = | 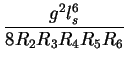 |
||
| = | |||
| G | = | 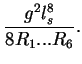 |
(27) |
This is agree with the result from GR.